|
OVALE DATI GLI ASSI |
| Dati | ASSE MINORE pari a 12 cm o secondo indicazione del docente |
| ASSE MAGGIORE pari a 18 cm o secondo indicazione del docente | |
| CONSEGNE: | |
| Consegna 1 | Esegui la costruzione geometrica come spiegato nel tutorial |
| Digit | Esegui le consegne in digitale utilizzando il CAD |
| DIFFICOLTA’ e CLASSE: | |
| Livello | Classe |
|
| STRUMENTI NECESSARI: |
 |
| DESCRIZIONE: |
Prima di iniziare, pulisci il piano di lavoro e gli strumenti da disegno. Usando un foglio F4 liscio, effettua la sua squadratura secondo lo schema appreso (vedi SQUADRATURA). Utilizzeremo l’area da disegno (quella gialla) per realizzare le consegne.
| FIGURA DI RIFERIMENTO: |
| PROCEDURA OPERATIVA |
posizionando il foglio in orizzontale (ossia con il lato lungo verso di noi), procediamo nel seguente modo:
Step #1 – tracciamo una retta orizzontale r a circa metà del foglio;
Step #2 – allo stesso modo tracciamo una retta verticale s a metà della retta r;

Step #3 – le due rette si incontreranno in un punto che chiameremo O; sulla retta r tracciamo l’asse maggiore di dimensioni note AB;

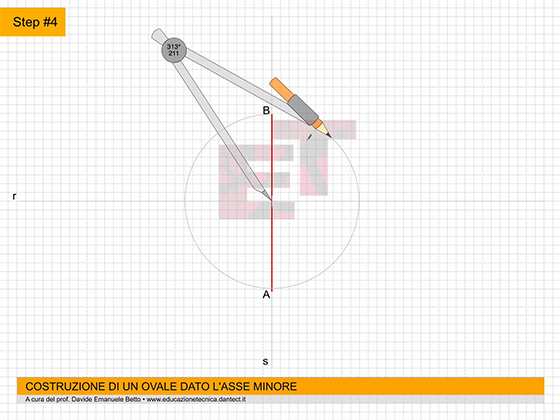
Step #4 – mentre su quella verticale s, tracciamo l’asse minore di dimensioni note CD;

Step #5 – adesso, puntiamo il compasso in O e con apertura pari a metà dell’asse minore OD, tracciamo l’arco che interseca l’asse maggiore AB nel punto 1;

Step #6 – uniamo con il righello i quattro estremi degli assi A-B-C-D tra di loro formando un rombo;
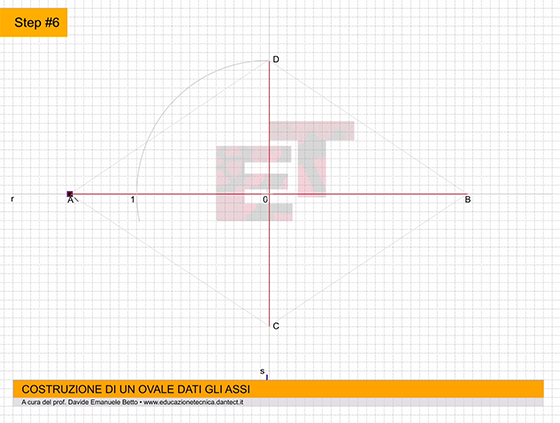
Step #7 – apriamo il compasso con apertura A1 e puntiamolo in D. Tracciamo un arco che interseca il segmento AD nel punto E e il segmento DB nel punto F;
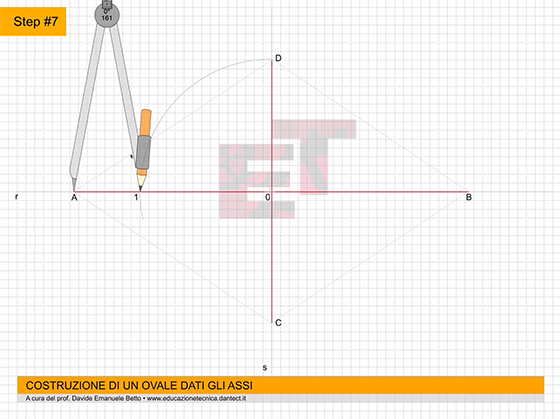

Step #8 – allo stesso modo puntiamo il compasso in C e con la stessa apertura, tracciamo un altro arco che interseca il segmento CA nel punto G e il segmento CB nel punto H;

Step #9 – osserviamo adesso il segmento AE, quello evidenziato in verde, e costruiamo la perpendicolare passante per il suo punto medio; puntiamo prima il compasso in A con apertura AE e poi in E con la stessa apertura e tracciamo due archi che si incontrano nei punti 2 e 3;


Step #10 – uniamo, adesso, i punti 2 e 3 e prolunghiamo la retta passante per questi due punti fino ad incontrare l’asse s nel punto P;

Step #11 – tracciamo una retta orizzontale passante per il punto medio di AE, ossia per M fino ad incontrare il segmento DB nel punto Q;
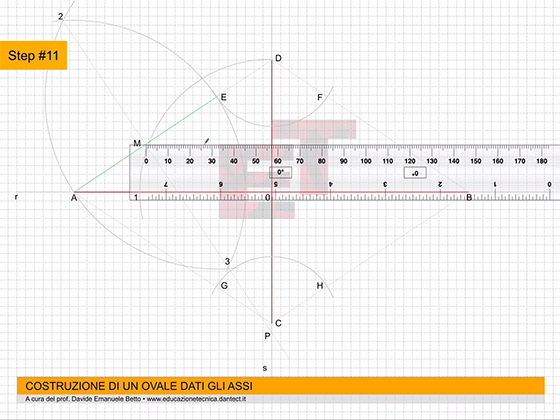
Step #12 – allo stesso modo tracciamo da M un segmento verticale fino ad intersecare il segmento AC nel punto N;

Step #13 – #14 – facciamo lo stesso da Q e da N per individuare il punto O sul segmento CB;
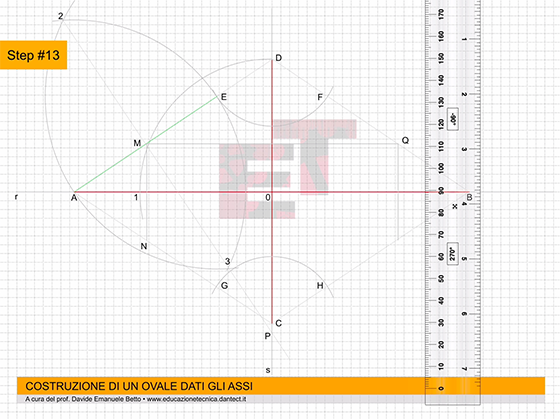

Step #15 – uniamo il punto N con il punto 4, intersezione tra la perpendicolare ad AE e l’asse r e prolunghiamolo fino ad incontrare l’asse s in un punto R;
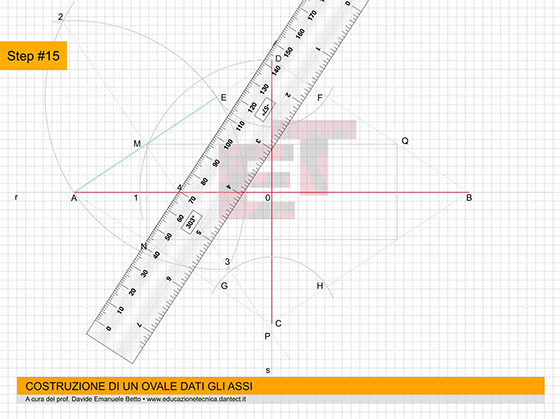
Step #16 – uniamo R con O per individuare sull’asse r il punto 5; ed infine Q con 5 fino a P;
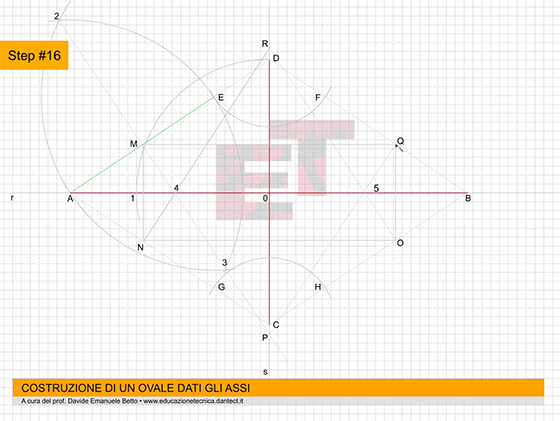
Step #17 – osserviamo adesso gli assi evidenziati in giallo che uniscono i punti 4 e 5, P ed R. Questi quattro punti sono i centri del nostro ovale; iniziamo la costruzione della nostra figura. Puntiamo il compasso con apertura 5B e tracciamo una porzione di arco come in figura;

Step #18 – in maniera speculare, puntiamo il compasso sul punto 4 e con la stessa apertura 4A, tracciamo un altro arco;

Step #19 – proseguiamo la nostra figura puntando il compasso in P e con apertura da P alla fine dell’arco precedente;
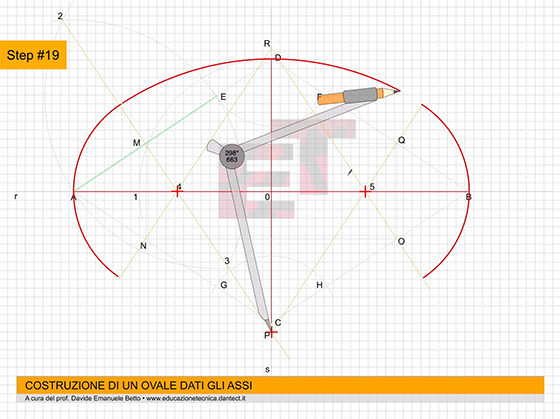
Step #20 – allo stesso modo puntiamo il compasso in R e con la stessa apertura completiamo la figura dell’ovale.

Ricordo che le linee colorate di rosso sono quelle che vanno rinforzate nel disegno.
| TUTORIAL VIDEO |












 Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.
Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.

 Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.
Questo esercizio non dispone di tutorial esplicativi perché presuppone la conoscenza delle tecniche di consegna. Si consiglia, quindi, di assegnarlo solo dopo aver fatto svolgere diversi esercizi e solo quando si riterranno i propri alunni capaci di poterlo svolgere autonomamente.